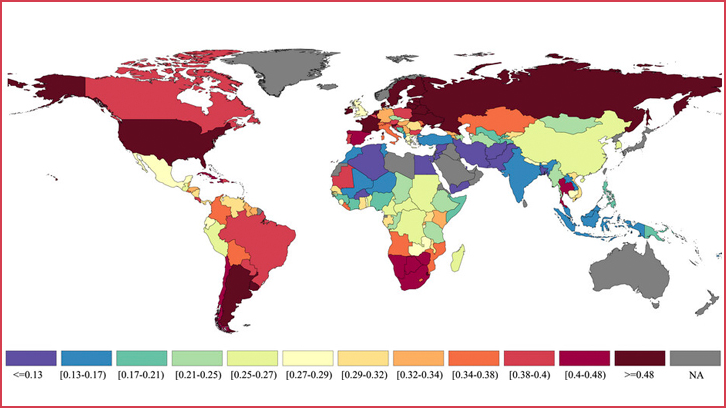
Caracterizadas diferentes nociones de posibilidad utilizando lógicas fuzzy
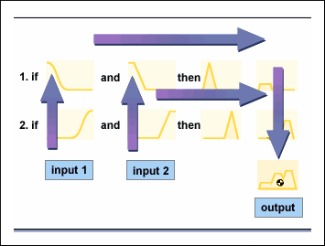
La representación de la información de origen humano y la formalización del CommonSense reasoning ha motivado diferentes escuelas de investigación en Inteligencia Artificial e Inteligencia Computacional durante la segunda mitad del siglo XX. Esta nueva tendencia ha situado la lógica formal, desarrollada originariamente en conexión con los fundamentos de la matemática, en una perspectiva completamente nueva, como herramienta para los ordenadores para procesar información. La lógica clásica ha puesto el énfasis tradicionalmente tanto en el procesamiento simbólico a un nivel sintáctico como en el nivel semántico, trabajando con dos valores de verdad.
La idea de los fuzzy sets introducida por L. A. Zadeh a principios de los 60 ha constituido un nuevo marco formal para capturar los grados de imprecisión en los dispositivos de representación de la información y del razonamiento. De hecho, los grados de pertenencia de los fuzzy sets pueden ser interpretados de maneras diferentes, todas ellas relevantes para el razonamiento humano, tales como niveles de intensidad, grados de similitud, niveles de incertidumbre o grados de preferencia. Es importante destacar que la fuzziness de una propiedad no debe verse como una carencia en la expresión lingüística del conocimiento (por ejemplo, falta de precisión, descuido, limitación de los lenguajes naturales ...), sino más bien como una forma de expresar la graduación.
El término fuzzy logic ha sido a menudo utilizado, no para tratar con grados de verdad, sino con grados de cualquier otro calidad o modalidad (posibilidad, entropía, necesidad e incluso, probabilidad). Así pues, durante mucho tiempo, la fuzzy logic ha sido (ya veces aún es) entendida como una caja de herramientas de ingeniería. Empujada por las aplicaciones, a menudo se encontraba carente de fundamentos (meta-) teóricos y de resultados generales; mayoritariamente desarrollada por ingenieros para propósitos particulares, ha sufrido de definiciones arbitrarias ya menudo, de imprecisión matemática. Durante los años 90 la situación comenzó a cambiar, principalmente gracias a los trabajos de S. Gottwald, P. Hájek, R. Cignoli, V. Novák, y de muchos otros lógicos matemáticos. Ellos desarrollaron sistemas de lógica multivaluada, que se convirtieron en formalismos adecuados para representando la fuzziness en el sentido de pertenencia a una propiedad gradual. Los esfuerzos hechos por estos investigadores culminaron en el establecimiento de la lógica fuzzy matemática como subdisciplina de la lógica matemática, un miembro respetable de la gran familia de lógicas no-clásicas.
Las t-normas continuas más importantes.
La lógica de Gödel es uno de los sistemas más prominentes de la fuzzy logic, es una extensión de la lógica intuicionista. El trabajo de investigación presentado en introduce diferentes lógicas para capturar las diferentes nociones de necesidad (en el sentido de la teoría de la posibilidad) por las fórmulas de Gödel. Basadas en diferentes caracterizaciones de las medidas de necesidad en los fuzzy sets, un grupo de lógicas con semánticas Kripke-style se definen sobre un lenguaje restringido, es decir, un lenguaje de dos niveles, compuesto por fórmulas no-modales y modales. En estas últimas no se permiten aniuaments del operador modal N. En el texto se prueba la completitud de la lógica y se demuestran algunos resultados de complejidad computacional.
Referencias
"Extending possibilistic logic over Gödel logic". P. Dellunde, L. Godo and E. Marchioni. International Journal of Approximate Reasoning. 52(1): 63-75, 2011.