UABDivulga - Barcelona recerca i innovació

Fractional Brownian motion (fBm) is a generalization of the more well-known Brownian motion process, and was originally introduced by Kolmogorov in 1940 in connection with turbulence modelling, although its name comes from the influential paper by Mandelbrot and Van Ness (1968). fBm is a stochastic process depending on a parameter H (in (0,1)), called "Hurst index" after the English hydrologist who studied the memory of Nile River maxima in connection of designing water reservoirs in 1951. Standard Brownian motion process corresponds to case H=1/2. This process is self-similar (or scale invariant) and in case H>1/2 the increments exhibit long-range dependence. This two properties made fBm play a very important role in modelling.

For instance, in network traffic can observed the presence of long-range dependence (called Joseph Effect) as well as that of self-similar patterns. One simple physical explanation for this is the superposition of many On/Off sources of fluid for the network, with strictly alternating On/Off periods and whose On/Off period lengths have high variability (or "heavy tails", this is called Noah Effect): Taqqu, Willinger and Sherman proved in 1997 that the superposition of many of that sources generates an aggregate cumulative (up to any time) arrival process that conveniently scaled converges in some sense to a fBm, and they relate the parameter that describes the intensity of the Noah Effect of the On/Off periods with the Hurst index of the fBm, that describes the intensity of the  Joseph Effect.

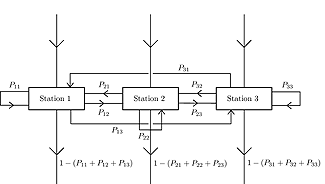
It is considered a non-deterministic fluid model on a network composed by J stations with a single server that processes fluid at a constant rate, under FIFO (first-in-first-out) discipline, and an infinite buffer at each one, with feedback (that means that a proportion of fluid leaving a station j goes next to any station k to be reprocessed, say Pjk, and the rest of fluid leaves the network). The figure shows the flow into and out of the network and between stations for the case J=3. The process of external arrivals is assumed to be a non-deterministic aggregated cumulative process generated by a large enough number of heavy tailed On/Off sources, similar to that of Taqqu et al.

In that scenario, we prove that after adequate scaling, the immediate workload process, that measures the congestion and delay in the network, defined as the amount of time required for any server to complete processing of all fluids in queue (or being processed) at any time,  converges to a J-dimensional fractional Brownian motion process reflected to be non-negative (because the workload is a non-negative process), under heavy traffic. Heavy traffic condition establishes that the total load imposed on each service station tends to be equal to its capacity of processing (that is, traffic intensity, defined as fluid rate through stations over processing rate, tends to be one).

This theorem is a generalization of a result of Debicki and Mandjes (2004) for fluid models on a network with a single station to a multi-station environment with feedback.

The interest of the paper is its contribution to stochastic modelling of network traffic and the study of multidimensional reflected fBm process in connection with it.