Un enfoque simple y analítico para el sintonizado robusto de controladores PID
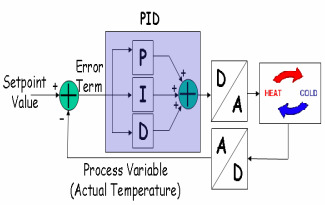
Un sistema de control realimentado negativamente permite mantener la salida de un proceso cerca del valor deseado aunque haya perturbaciones. La estrategia más común es obtener primero un modelo matemático para el proceso a controlar y, en base a este modelo, sintonizar el algoritmo de control. En contraposición a muchos métodos de tipo empírico, este artículo propone una manera analítica de sintonizar un controlador de tipo PID en base a un modelo de primer orden más tiempo muerto. El objetivo es la obtención de respuestas suaves.
Un sistema de control realimentado negativamente se compone de dos componentes básicos: el proceso físico (o planta) P y el controlador K. El proceso tiene una entrada, denominada variable de control y denotada por u. La salida del proceso se denota por y, y es la variable controlada. La lectura de esta variable normalmente proviene de algún sensor.
El objetivo del sistema es mantener la salida del proceso cerca de un cierto valor deseado o de referencia, denotado por r. Por lo tanto, lo que interesa es mantener pequeño el error e = r - y a lo largo del tiempo aun cuando se puedan producir perturbaciones en el sistema, denotadas por d. El controlador K tiene una entrada, el error e, y una salida, la señal de control u. La idea de la realimentación (feedback en inglés), a pesar de su sencillez, es extremadamente útil. Un ejemplo sencillo viene dado por un termostato: cuando la temperatura en un cuarto llega a un cierto umbral superior (r + e), el termostato se desactiva para que la temperatura empiece a bajar. Cuando la temperatura baja hasta un cierto umbral inferior (r - e), el termostato se vuelve a poner en marcha. De esta manera, una cierta temperatura promedio (r) se va manteniendo. Podemos expresar esta estrategia de control matemáticamente:
donde umax representa la acción de control que se usa cuando el termostato está activo. La razón por la cual la realimentación negativa es tan interesante es porque permite mantener la salida del proceso cerca del valor deseado aunque no haya perturbaciones (pensemos que alguien abriera una ventana en la habitación donde tenemos el termostato) o cambios en el proceso a controlar. A nivel industrial, el algoritmo de control más empleado tiene la forma:
y de aquí su nombre: Proporcional-Integral-Derivatiu (PID). El procedimiento de encontrar el valor de los parámetros K, Ti, Td se denomina sintonizado. Aun cuando existen muchas reglas de sintonía para controladores PID, cada año aparecen nuevas. En parte esto es debido al uso tan extendido de este tipo de controladores en la industria, donde los beneficios de mejorar las sintonías pueden ser considerables. La estrategia más común es obtener primero un modelo matemático para el proceso a controlar y, en base a este modelo, sintonizar el PID. Es siempre conveniente considerar el modelo más sencillo posible. En esta línea, un modelo de tres parámetros muy sencillo para el proceso P es el denominado de Primer Orden con Tiempo Muerto. La respuesta de este modelo ante un escalón unitario, definido como se muestra en la figura de abajo
donde Kp, t, h, son, respectivamente, la ganancia, la constante de tiempo y el tiempo muerto (o retardo) del proceso. La constante de tiempo es el tiempo que tarda el sistema en lograr el 63.2% de su valor final (Kp veces la magnitut del escalón en la entrada, en este caso 1) a partir de que el retardo (h) ha transcurrido. En la figura, Kp = t = h = 1. Si suponemos que la distribución de la temperatura en la habitación del termostato es lo suficiente homogénea, la gráfica de arriba podría cogerse como un modelo de parámetros concentrados para la evolución de la temperatura ante un incremento escalonado en la energía entregada por el suministro de calor.
En contraposición a muchos métodos de tipo empírico, este artículo propone una manera analítica de sintonizar un controlador de tipo PID en base a un modelo de Primer Orden más Tiempo Muerto. El objetivo es la obtención de respuestas suaves: queremos que la salida del sistema siga la referencia lo más rápido posible evitando soprepicos (se produce sobrepico cuando y supera el valor de referencia r). La suavidad también hace referencia a que la acción de control no cambie de manera excesivamente brusca, evitando echar a perder los sistemas de actuación.
Referencias
"Simple Analytical min-max Model Matching Approach to Robust Proportional-Integrative-Derivative Tuning with Smooth Set-Point Response". Alcántara, S; Pedret, C; Vilanova, R; Zhang, WD. INDUSTRIAL & ENGINEERING CHEMISTRY RESEARCH, 49 (2): 690-700 JAN 20 2010.